Для знающих математику
- Найдите наименьшее число
Найдите наименьшее число, которое при делении на числа 2, 3, 4, 5, 6, 7, 8 и 9 дает, соответственно, в остатке числа 1, 2, 3, 4, 5, 6, 7 и 8.
- Сколько рыб в пруду?
Рыбаки выловили сетью из пруда 60 рыб, отметили их и снова бросили в воду.
На другой день рыбаки выловили сетью 80 рыб. Среди них 5 оказались мечеными. Можно ли по этим данным сказать, сколько всего рыб в пруду?
- Принесите воду
Есть два ведра емкостью 4 и 9 литров. Как с их помощью принести из речки ровно 6 литров воды?
- Какое число
Какое число нужно прибавить к числам 100 и 164, чтобы обе суммы были квадратами целых чисел?
- Найдите число
Некоторое число оканчивается на «2». Если цифру «2» переставить из конца числа в начало, то получится число, которое в два раза больше первоначального. Найдите это число.
- Не пользуясь семеркой
| 2 | * | * | ||
| x | 3 | * | * | |
| 5 | * | * | ||
| * | 4 | * | ||
| * | * | 3 | _ | _ |
| * | * | * | * | * |
В примере на умножение надо заменить звездочки цифрами.
Цифра «семь» не встречается ни разу.
- Вдоль экватора
Самолет, вылетев из пункта, расположенного на экваторе, облетает по экватору Землю с востока на запад. Пилот вылетает точно в момент восхода солнца и летит только днем. С заходом солнца он приземляется и отдыхает. Какова скорость самолета, если пилот возвращается в первоначальный пункт в момент восьмого захода солнца? Длина экватора 40 000 км. Скорость самолета принимаем постоянной.
- Разделите вино
В бочонке десять литров вина. Как с помощью двух ведер емкостью 3 и 7 литров разлить это вино по 5 литров?
- Семерка из двоек
Как при помощи пяти двоек получить число семь?
- Девятка из десяти цифр
Сможете ли вы получить число «9», пользуясь всеми десятью цифрами: О, 1, 2, 3, 4, 5, 6, 7, 8, 9?
- Яблоки
Петя получил 1/3 часть всех яблок и еще два яблока, Сережа — 1/4 часть всех яблок и одно яблоко, а Коля — половину оставшихся яблок. В результате осталась 1/6 часть первоначального количества яблок. Сколько яблок получил каждый из детей?
- Из Будапешта в Волгоград
Самолет летит из Будапешта в Волгоград (эти города находятся приблизительно на одной и той же географической широте) по кратчайшему воздушному пути. Остается ли постоянной географическая широта самолета при его движении?
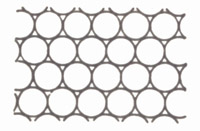
- Из листа железа
Из листа железа нужно вырезать много небольших кружочков. Материал, оставшийся между кружками, идет в отходы. Как должны быть размещены
круги на листе железа, чтобы отходы были минимальными? Как вы расцениваете решение, показанное на рисунке?

Ответы
- Найдите наименьшее число
Искомое число — 2519.
- Сколько рыб в пруду?
Во втором улове общее число рыб превосходит число меченых в 16 раз. Если считать, что меченые рыбы равномерно распределены среди всех остальных рыб, то общее число рыб в 16 раз больше общего числа меченых рыб. Следовательно, в пруду: 60 X 16 = 960 рыб.
- Принесите воду
Из полного девятилитрового ведра нужно вылить в реку 8литров воды, пользуясь ведром в 4 литра. Затем литр, оставшийся в большом ведре, нужно перелить в пустое четырехлитровое ведро. Если в него теперь добавить три литра из полного большого ведра, то в девятилитровом ведре как раз останется шесть литров воды.
- Какое число
Нам надо найти такое число х, чтобы 164 + х = а2 и 100 + х = в2. Здесь а и в — целые числа, причем а > в, а >12, в >10, а + в > 22. Вычтем из первого уравнения второе. Получим: 64 = (а+в)(а-в). Если а+в=64, а а - в=1, то 2а=65. Этого быть не может, так как а — целое число.
Рассмотрим другой вариант:
а + в = 32, а - в =2. Отсюда а=17, в=15. Это удовлетворяет условию
задачи, следовательно, х = 125.
- Найдите число
Задача имеет бесчисленное множество решений. Вот одно из них: 105 263 157 894 736 842
- Не пользуясь семеркой
| х | 2 | 8 | 1 | |
| __ | __ | 3 | 3 | 2 |
| 5 | 6 | 2 | ||
| 8 | 4 | 3 | ||
| 8 | 4 | 3 | __ | __ |
| 9 | 3 | 2 | 9 | 2 |
- Вдоль экватора
На экваторе долгота дня равна долготе ночи и составляет 12 часов. По условию задачи, пилот находился в воздухе 8 дней. Следовательно, продвигаясь на запад, он в течение одного дня покрывал расстояние, равное 1/8 длины экватора, и приземлялся в таком пункте, где солнце заходило на 3 часа позже (24:8) по сравнению с пунктом вылета. Поскольку самолет ежедневно приземлялся при заходе солнца, время нахождения его в воздухе составляло 12 + 3 = 15 часов в сутки, а всего — 8 х 15 = 120
часов. Таким образом, скорость самолета:
40000 : 120 = 333 км/час.
- Разделите вино
Надо наполнить семилитровое ведро при помощи трехлитровой посуды, наливая в нее вино каждый раз доверху.
В конце этой операции мы будем иметь: в бочонке — 1 литр вина, в трехлитровом ведре — 2 и в семилитровом — 7 литров вина. Теперь надо вылить вино из семилитрового ведра назад в бочонок, а 2 литра вина из трехлитрового ведра перелить в пустое семилитровое. Если теперь туда же перелить из бочонка 3 литра вина при помощи трехлитровой посуды, то в бочонке и в семилитровом ведре окажется по 5 литров вина.
- Семерка из двоек
2 X 2 X 2 - 2:2 = 7.
22 : 2 - 22 = 7.
- Девятка из десяти цифр
Вот несколько возможных решений:
97524 : 10836 = 9
95823 : 10647 = 9
95742 : 10638 = 9
0 х 12346678 + 9 = 9
1234567890 + 8 = 9
- Яблоки
Петя получил 14 яблок, Сережа — 10, а Коля — 6.
- Из Будапешта в Волгоград
Нет. На шаре кратчайший путь между двумя любыми точками — дуга большого круга, соединяющая эти две точки. Широта самолета оставалась бы постоянной только в том случае, если бы он летел по параллели.
- Из листа железа
Наилучшее решение показано на рисунке.